A quelle distance se trouve l'horizon lorsqu'on regarde l'Océan ?
Du fait de courbure de la Terre, notre regard ne peut porter qu'à une distance limitée lorsque nous nous trouvons face à l'océan.
Plus l'altitude du point d'observation, ou d'émission dans le cas des émetteurs de télévision ou FM, est élevé, plus la distance de vision est importante. On parle aussi de ligne d'horizon visuelle ou hertzienne.
C'est pour cette raison que très tôt les feux des phares ont été placés dans des positions aussi élevées que possible malgré l'augmentation de coût que cela impliquait dans leur construction, et que les hunes d'observation des navires étaient placées en haut du plus grand mât.
Pour un homme de 1,80 mètre situé au bord de la mer, l'horizon se trouve à environ 4 789 mètres seulement.
Pour ceux qui veulent s'amuser à faire des calculs, la formule est simple, C'est celle de la puissance d'un point par rapport à un cercle :
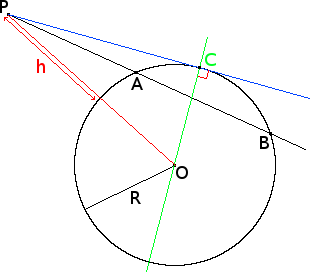
On démontre en effet que quel que soit le segment sécant mené d'un point P extérieur à un cercle de centre O, de rayon R et le coupant en des points A et B, on a PA x PB = constante = PO² - R².
Le point limite de vision est le point situé sur la droite qui passe par le point P et qui est tangente à la Terre, cas particulier avec A = B.
Le rayon de la Terre étant de 6 371 km, on calcule facilement que :
d = (racine carrée)h x (12742 + h)
(d, la portée et h, la hauteur, étant exprimés en kilomètres).
Et pour info si l'horizon était plat on pourrait voir la lueur d'une bougie jusqu'à environ cinquante kilomètres
@Tokooran: Horizon arrondi = terre ronde, Horizon plat = terre plate. Je pense que c'est plutôt censé ce qu'il raconte.
@Tokooran: C'est bien d'une surface plate qu'il parle (enfin je pense).Compliqué de trouver une surface plate de 50km en revanche.
@Blazdack: Sauf que même si la Terre était plate, je vois difficilement comment la lumière d'une bougie seule pourrait traverser cinquante kilomètres d'atmosphère sans se disperser...
@Tokooran:
En fait, Les photorécepteurs de la rétine sont très nombreux en périphérie de celle-ci.On capte donc plus de lumière en ne regardant pas directement une source lumineuse (Je te conseille d'essayer avec un étoile la nuit, c'est flagrant).
Il faut aussi prendre en compte que la pupille humaine se dilate à son maximum après environ 30 minutes d'obscurité, ce qui permet à la rétine de recevoir encore plus de lumière.
Bien sur, pour voir une bougie à 50km, les conditions atmosphérique devraient être optimales et encore un fois, une surface plane de 50km est introuvable sur Terre.
Un complément et une capture d'écran ici : http://www.udppc.asso.fr/bupdoc/consultation/article-bup.php?ID_fiche=21965
@Tokooran: L'air agit presque comme le vide concernant la propagation des ondes électromagnétiques, à savoir que l'air est vraiment peu dispersif, donc l'atténuation d'une onde EM est vraiment négligeable devant les autres grandeurs mises en jeu.
Le problème vient plutôt de l'intensité lumineuse qu'est capable d'émettre la bougie.
Sous certaines hypothèses(réalistes) quant à la capacité de notre rétine à recevoir un flux lumineux, on peut montrer, que dans le noir, à une distance de 50km, sur terrain plat, une intensité d'1 candela est suffisant à "avoir la sensation" d'une source lumineuse.
Pourquoi on simplifie pas directement
(E) = PO²-R² = (R+h)²-R² = 2hR +h²
Question sans prétention je suis juste curieux. J'suis pas aller retrouvé (E) et je l'ai accepté en tant que tel, mais voilà si c'est un résultat avéré pourquoi ne pas le simplifier ?
@Gerceval: C'est bien joli un polynôme, surtout développé je suis d'accord ! Mais pour pousser le vice plus loin, on peut négliger h² car très petit par rapport à 2hR. On obtient grossièrement d = sqrt(2hR). Là, je pense qu'elle est simplifiée !
@Gerceval: Et pourtant, les négligences et équivalences, c'est quelque chose de très mathématique ... Si tu savais !
Tu m'as fait galérer avec la mise en forme de ta formule, comme ça c'est plus compréhensible:
D = sqrt(2hR + h2)
ps: sqrt = square root = racine carrée.
@Oznek: Pour les adeptes des logiciels de calcul, on préférera d = (P.h+h^2)^1/2 où P = 2.R et en remplaçant les points par des asterisques.
@pseudotemporair: Et tu fais comment pour que ça apparaissent dans le descriptif de la box ?J'ai bien saisi ? mais quand la box a été intégrée, ça s'est transformé en ?.
"Démonstration" simple (Pythagore) dans le cas où A et B sont identiques, le regard décrivant donc une droite tangente au cercle passant par C (petit schéma en prime pour ceux qui n'ont pas les idées claires) :
PO² = R² + PA²
or PO = h + R, h hauteur des yeux, donc
(h + R)² = R² + PA²
PA = sqrt( h² + R² + 2hR - R² )
PA = sqrt ( h(h+2R) )
Par contre dans le cas général où A!=B je ne sais pas...
@SetaTroller: oui ainsi que la position et l'angle des yeux sur le visage qui varie énormément dans la race humaine
Tu ne dois accéder à ce site que si tu as au moins 18 ans ou si tu as l'âge légal pour visionner ce type de matériel dans ta juridiction locale, l’âge le plus élevé étant retenu. En outre, tu déclares et garantis que tu ne permettras aucun mineur à d'accéder à ce site ou à ces services.
En accédant à ce site, tu acceptes nos conditions d'utilisation.