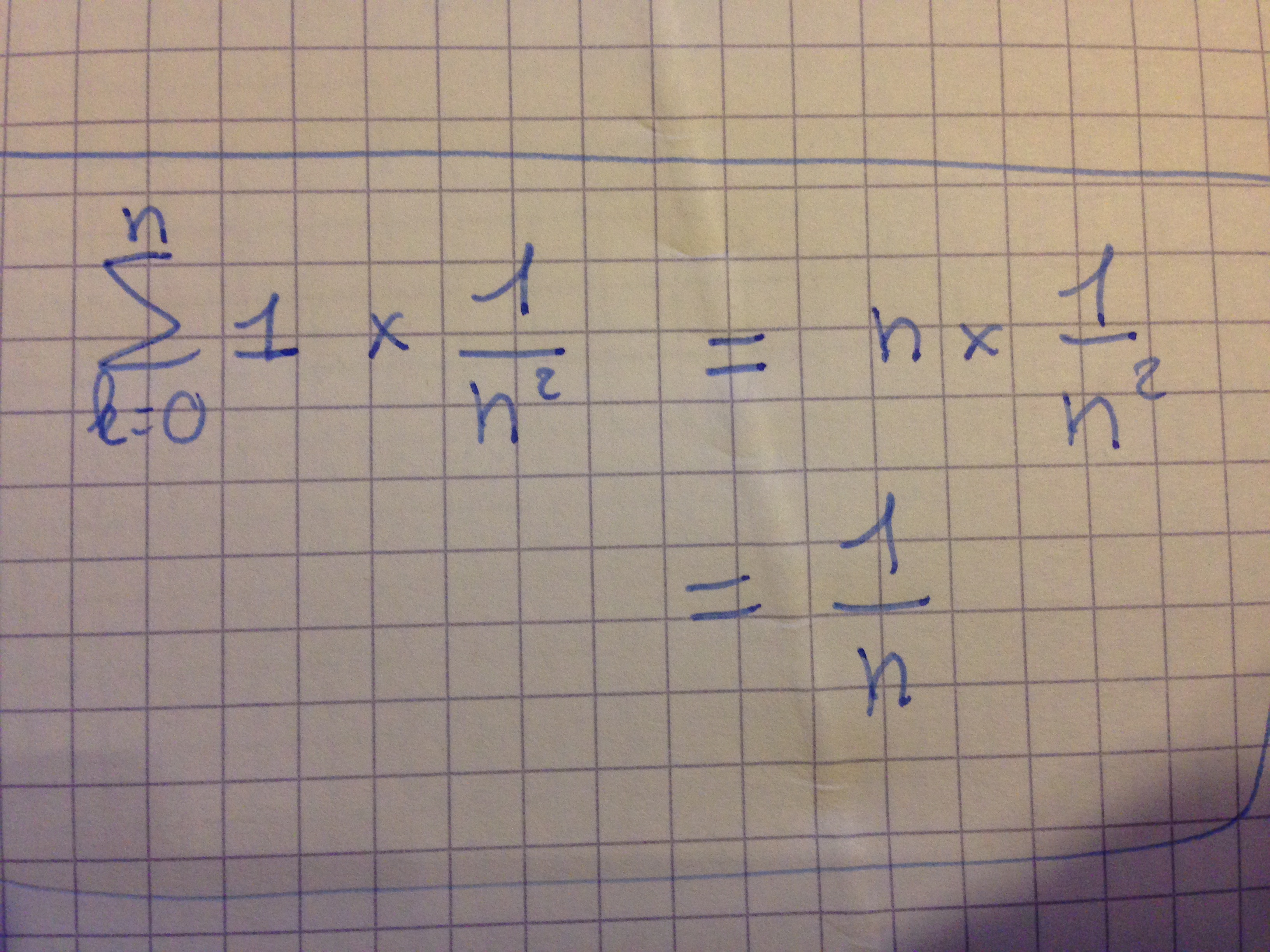[Maths Terminale S] Sommes arithmétiques et égalités
Bonjour les matheux !
J'aimerai juste savoir si ce raisonnement est mathématiquement juste et sinon à quel moment est-il faux (2 ou 3).
Merci d'avance ! :)
Incube
![[Maths Terminale S] Sommes arithmétiques et égalités](https://static.choualbox.com/Img/141122934446.jpg "3264x2448 - 1832ko")
Y-a-il moyen d'avoir le sujet ? Cela aide souvent beaucoup pour la résolution.
Sinon, pour moi, ton passage de la deux à la trois est faux.
Tu ne peux pas virer le symbole somme comme ça. Alors certes, il n'y a pas d'indice "k" dedans, mais qu'est-ce que cela veut dire ? Essaye de factoriser pour voir.
Mon but est d'encadrer la somme à la dernière ligne et j'ai comme information la première ligne, je cherche un raisonnement pour y arriver.
Alors effectivement, si le terme général de ta suite (Un) correspond à l'élément encadré de ta deuxième ligne, tu as raison de passer de la ligne 1 à la 2 de cette manière.
Le problème est sur la ligne 3, regarde bien : c'est plutôt choquant, non ? Ce que tu dis, c'est que la ligne 1 et la ligne 3 sont parfaitement équivalentes.
Ce qui est faux, c'est que tu dis que "la somme de 1/(2n^2) pour k allant de 0 à n est égale à 1/(2n^2). Ainsi que pour la somme de (1/n^2). C'est une simple erreur de calcul, tu devrais facilement trouver ;)
Le truc c'est que je n'ai pas encore fait de cours sur les sommes, Sigma d'un nombre n'ayant pas de réel k ne me dis absolument rien... Je vais réfléchir
Alors justement, il n'y a pas de k. Ça peut te paraître déroutant. Mais est-ce que ça l'est vraiment ? Après tout, on peut factoriser par tout ce qui n'a pas de "k", non ? Et alors, qu'est-ce qui va rester du coup ?
Pour passer de 2 à 3 faut que tu calcules les sommes de gauche et droite, là t'as juste viré le sigma, si tu vois pas comment faire le calcul réfléchie à ce que donne la somme des n 1er termes d'une suite constante égale à 1.
