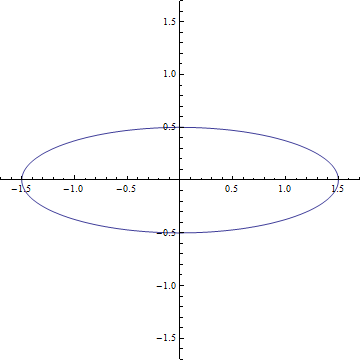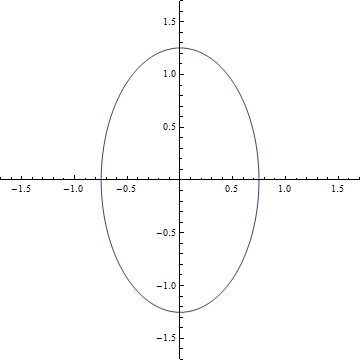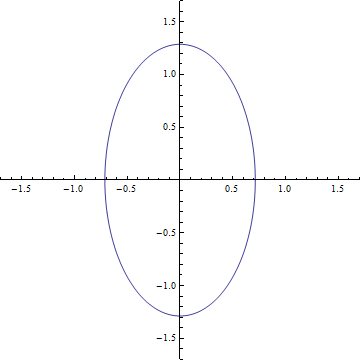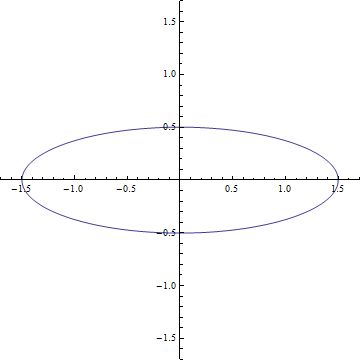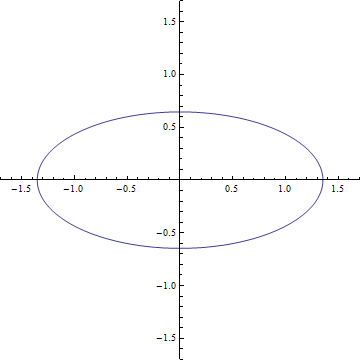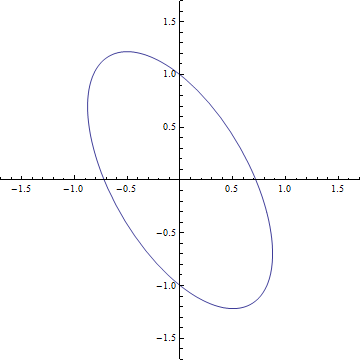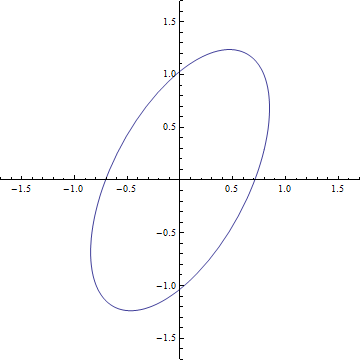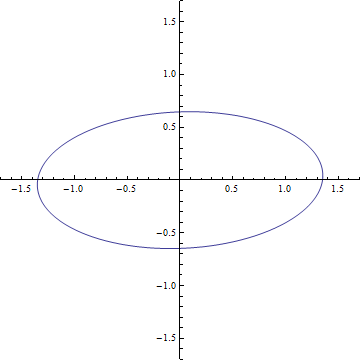Les ondes gravitationnelles
Lors d’une précédente box, j’ avais brièvement parlé du futur détecteur d’ondes gravitationnelles eLISA. Dans une suite logique j’essaierai ici de dresser une toute petite introduction à l’univers des ondes gravitationnelles.
Avant toute chose il faut d’abord saisir le cadre physique qui englobe ce concept. Les ondes gravitationnelles sont prédites par la théorie de la relativité générale dont je ne parlerai pas puisqu’un épisode d’e-penser lui est dédié, est très bien fait et je ne prétends pas à sa capacité de vulgarisation.
Cette théorie nous permet donc d’écrire une équation reliant la géométrie de l’espace-temps (tenseur d’Einstein) à son contenu en énergie (tenseur d’énergie-impulsion). Le problème de cette équation est la difficulté voir l’impossibilité d’en trouver des solutions analytiques (résoudre l’équation et obtenir une solution qu’on écrit en terme de fonctions analytiques – f(x) = sin(x), f(x) = x²,… par exemple sont des fonctions analytiques) sauf dans quelques cas.
La simulation numérique permet d’approcher ces solutions autant qu’on veut mais rien de tel que d’avoir des solutions que l’on puisse étudier avec un papier et un crayon au dos d’une enveloppe. Pour cela, une méthode souvent utilisée est celle de la linéarisation des équations. On va rendre les équations plus simples en négligeant les termes qui nous embêtent. Dans l’équation d’Einstein cela peut se faire en supposant un champ de gravitation faible, une faible déformation de l’espace-temps. En développant ainsi les équations on tombe sur une équation qui ressemble presque identiquement aux équations de Maxwell qui décrivent les ondes électromagnétiques. La différence réside dans le fait qu’au lieu d’avoir un vecteur qui décrit le champ électromagnétique on a un « tenseur » (une matrice, en très gros) qui décrit l’espace-temps et au lieu d’avoir un courant on a le tenseur énergie impulsion.
Pour simplifier encore plus on va travailler dans le vide et on se débarrasse ainsi du tenseur énergie impulsion. On tombe alors directement sur une équation qui décrit l’évolution d’une onde, la propagation d'une déformation de l’espace temps !
On peut alors étudier les caractéristiques de cette onde et on remarque qu’elle se déplace à la vitesse de la lumière, qu’elle a deux degrés de liberté (son évolution est guidée par deux paramètres distincts) et qu’elle est transversale (elle oscille perpendiculairement à la direction de propagation de l’onde dans l’espace-temps).
On peut ensuite calculer ce qu’elle engendrerait comme déformation. Pour cela on construit un anneau de matière parfaitement circulaire et on imagine que l’onde se propage dans la direction perpendiculaire au plan de l’anneau. On obtient alors un résultat qui est donné sur le gif (que je me suis fait chié à faire). En fait on peut développer deux résultats qui correspondent aux deux degrés de liberté et voir que c’est le même incliné de 45 degrés. On peut alors comprendre comment fonctionne le détecteur. Imaginez qu’on place les 3 satellites d’eLISA sur le cercle de départ, quand l’onde va passer le cercle va se déformer et les détecteurs vont alors mesurer une variation de leur inter-distance.
En fait, l’analogie avec l’électromagnétisme est très forte. On retrouve l’idée de polarisation de la lumière au travers les deux degrés de liberté. On peut ainsi retrouver les polarisations circulaires et linéaires. Le gif représente ainsi une polarisation linéaire et pour une polarisation circulaire on verra l’anneau de matière déformer en ellipse tourner autour du centre.
On peut également démontrer l'existence d'ondes gravitationnelles pour la version non-linéarisée (non-simplifiée) des équations d'Einstein et certaines solutions exactes ont même été trouvées.
J’espère que cela vous aura permis de mieux comprendre le fonctionnement du détecteur et la nature de ces ondes! N’hésitez pas si vous avez des questions.
Sources :
- Misner, Gravitation (Freeman, 1973) (mp si vous voulez le pdf)
- http://arxiv.org/abs/0709.4682 (une introduction aux ondes gravitationnelles)
- http://choualbox.com/VI6Gd (la box à laquelle je fais référence au début)
ps : Les deux autres grands types de polarisation des ondes gravitationnelles en commentaires.
J'ai compris que tu essayais de m'apprendre un truc et que cela était intéressent mais j'ai pas réussie à tout lire...
Mais juste pour savoir, ça apporte quoi de savoir ça au juste ? Ça a une réelle utile dans l'application de quelque chose plus tard ou c'est juste pour prouver que quelque chose existe uniquement ?
En astrophysique, un des gros problème est que la lumière est atténuée par les nuages de gaz,... donc ils sont limités dans leurs observation par ce facteur. Comme les ondes gravitationnelles interagissent très peux avec la matière elles permettent de faire des observation beaucoup plus dans l'espace (et donc dans le temps). Ça permettrait également par exemple de détecter la fusion de trous noirs massifs qui en émettent énormément.
Il existe une expérience sur Terre qui essaye (en vain) de détecter les ondes gravitationnelles à l'aide d'un interféromètre de Michelson géant : Virgo. Plus d'info ici : http://www.cnrs.fr/cw/dossiers/dosbig/decouv/xoutil/outilMod/1_1/niv1_1.htm
Oui, il y aussi LIGO mais je n'en parle pas ici parce que je l'avais déjà évoqué dans la box précédente :)
Ça m'a rappelé mes cours sur les ondes électromagnétiques (polarisation, etc...) ! Sauf que considérer la même chose dans le cadre d'un champ gravitationnel me paraît vraiment fou... Je connais la théorie (dans les grandes lignes seulement, évidemment), mais cela reste vraiment impressionnant. Et dans quelques années on annoncera peut être la découverte du graviton...
Super, merci beaucoup c'est très intéressant !
Question surement bête, mais cette expérience pourrait elle nous en apprendre plus sur le vecteur potentiel de gravitation (le graviton) ?
C'est loin d'être une bête question :) Ce que je sais c'est que si on détecte bien ces ondes et qu'on observe cette symétrie par rotation de 45 degrés (prédite par la relativité générale) alors on a que le graviton doit être de spin 2 en théorie de champ faible. Maintenant je ne m'y connais pas assez sur ceux-ci pour te donner une réponse correcte! Je vais m'informer de mon côté :)
J'aurais misé sur un spin de 1 ! (comme le photon ou le gluon vu que ce sont des luxons et que le graviton en serait un vu que l'onde gravitationnel va à la vitesse de la lumière).
En tout cas continue tes box sur le sujet, c'est passionnant !
Alors dis moi si j'ai compris mais en très très gros ça fonctionne comme pour détecter les tremblements de terre, sauf que là on va détecter les "tremblements"/déformation de l'espace temps.
C'est assez péchu, ici c'est choualbox, c'est pipi nazi caca bite cul etc...
Pas vraiment en fait. Il me semble qu'on détecte des tremblements de terre en mettant plusieurs stations qui vont mesurer l'intensité des oscillations à un endroit précis pour les comparer. Quand une onde gravitationnelle passe tu n'as pas le même effet. Dans ce cas là on regarde la variation de la distance entre les satellites (le temps de trajet mis par la lumière pour revenir). Pour les tremblements de terre, tu ne regardes pas ça je pense.
Bah j'aime le cul et pourtant ça m'intéresse donc pourquoi pas les autres?
Son analogie est bonne, tu regardes pas le même type de variations mais grosso modo c'est comparable. Dans les 2 cas tu regardes les variations d'une quantité lors du passage d'une onde (sismique ou gravitationnelles).
Je ne suis pas tout à fait d'accord. Forcement une onde va se détecter par la mesure d'une variation périodique puisque c'est la définition d'une onde. Donc à ce titre sa comparaison est bonne mais est trop générale. Mais le principe de sa détection est complètement différent.
Forcement que le principe de détection est différent, ce ne sont pas les mêmes observables mais le concept général est le même. Je crois qu'on est d'accord enfaite :)